线性代数是数学的一个重要分支,它经常被施加到project问题,要了解学习和工作深入研究的深度,因此,对于线性代数的深刻理解是非常重要的。下面是我总结的距离DL book性代数中抽取出来的比較有意思的一些理解基础线代问题的还有一些很形象易懂的思路。
2.3 Identity and inverse matrices
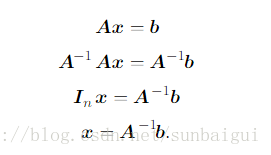
在实际应用场景中,当中inverse matrice
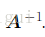
不一定能找到。另外找到的话也不一定能在数字电脑中精度无损的保存下来。
2.4 Linear dependence, span, and rank
为了求解方程
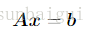
我们还能够从另外一个角度去看这个问题,我们把矩阵A中的每一列看成是一个方向,那么上述方程就能够看成是怎样从原点(全0)到达b,每次走都仅仅能沿着A中每一列所代表的方向。从这个角度去思考的话,上述方程能够写成例如以下形式:
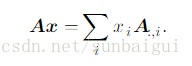
所以 假设想要对于不论什么的b(n维度)都能找到相应的解x(m维度)的话。那么n-D空间中的随意一个向量都能通过线性组合A(nxm维度)矩阵中的m列来得到,所以矩阵A的列数一定要大于等于其行数;假设将A矩阵看成是n条方程组成的方程组,那么仅仅有当方程组个数小于等于未知数个数时才干确保该方程组有解。在该方程的求解中假设 要找到A矩阵的逆作为该方程求解的工具,那么A矩阵必须是方形矩阵而且每一列都是列独立的。
线代中另一些很重要的概念会被用到。但在alexnet提出的CNN网络中的话也已经够用了; 另外的话怎么样去设计loss函数然后计算其gradient用于backward propagation时的更新用到了其它的一些线代知识,我将在之后的博文中针对怎样使用梯度下降法优化损失函数进行探讨。
版权声明:本文博主原创文章。博客,未经同意不得转载。